MATEMÁTICA NA ANTIGUIDADE: ORIENTE MÉDIO – PARTE I

Por: Wellington Schühli De Carvalho

Tudo que sabemos da história vem de fontes e os mesopotâmios deixaram muitos registros através dos utensílios e tabletes de argila, com alguns datando de cerca de 4000 anos A.C.. Neste texto utilizaremos o termo mesopotâmico, pois trataremos da matemática de povos que viviam nessa região, entre eles os babilônicos.

Uma das motivações para a criação de um raciocínio matemático era o comércio: como realizar a troca de mercadorias e o seu armazenamento influenciou de maneira direta os povos para o começo de uma matemática primitiva. Um exemplo deste pensamento são os utensílios utilizados na economia para manter controle sobre os produtos, ou seja, os tokens. Estes objetos de argila apresentavam diversos formatos: cones, esferas, discos, cilindros, etc. e cada um estava associado a uma unidade ou quantidade de um tipo de insumo, por exemplo, uma jarra de óleo poderia ser contada com um ovoide, duas jarras de óleo poderiam ser contadas com dois ovoides e uma pequena quantidade de trigo era representada por uma esfera. Os tokens eram guardados em invólucros de argila e marcas eram feitas no exterior com os próprios tokens nas formas contidas no seu interior. Trata-se de uma maneira de contar bem rudimentar.

Figura 01 - Tokens e invólucro. Fonte: www.utexas.edu

A substituição de tokens por impressões foi o primeiro passo para a escrita. Na mesopotâmia a origem da escrita está amarrada com a origem da matemática, principalmente com a necessidade de contar. A primeira mudança é de impressões dos invólucros para os tabletes de argila. Um trabalho que já era feito nos invólucros, agora não há mais a necessidade de guardar os tokens. Nessa mudança os símbolos associados ao insumo ainda persistem, é preciso uma noção de abstração para utilização de quantidades para qualquer elemento. Com o decorrer do tempo houve outra mudança, as marcas que representavam quantidades eram acompanhadas de ideogramas que referiam aos objetos que estavam sendo registrados. Há aqui um grande avanço em relação a abstração. É um grande passo para a escrita, pois os registros das quantidades poderiam servir para coisas de naturezas diferentes.

A região possuía uma economia intensa e com a representação de números surge a necessidade de usar sistemas de medidas. Os tabletes mostram que na mesopotâmia havia mais de seis sistemas de capacidade usados para diferentes tipos de grãos e líquidos. Objetos discretos – por definição objetos discretos são aqueles que podem ser enumerados por inteiros. – eram contados na base 60, outros produtos eram contados na base 120 e existiam métodos para contar tempo e áreas. Os símbolos usados para a contagem no sistema de medida eram símbolos chamados de protocuneiformes, pois antecederam as escrita cuneiforme.

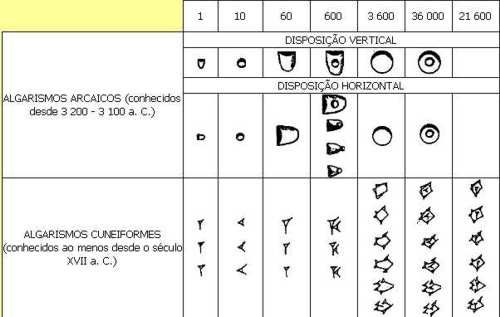Figura 02 - Algarismo protocuneiformes e algarismos cuneiformes. Fonte: portaldoprofessor.mec.gov.br

Figura  03: tablete com escrita cuneiforme. Fonte: Wikimedia.com

Ao final do terceiro milênio o sistema se estabiliza e neste momento ocorreram duas mudanças fundamentais. A primeira delas, a função de contagem de objetos discretos que os sinais tinham no sistema protocuneiforme, foi transformada e eles passaram a ser usados para fazer cálculos. A segunda mudança é que o mesmo sinal passou a ser usado para representar valores diferentes.

Os babilônios usavam dois símbolos, que poderiam representar qualquer número dependendo de sua posição. É o sistema sexagesimal posicional. O mesmo número poderia ser utilizado para representar 1, 60 e 3600 e outro símbolo poderia ser utilizado para representar 10, 600 e 36000. Podemos observar que os babilônios usavam uma combinação de base 60 e 10, pois os sinais mudam de 10 em 10. É um sistema aditivo, pois para construir alguns números é necessário repeti-los.

Figura 04: Números mesopotâmicos. Fonte: Wikimedia.com

Figura 05: Números Babilônios. Fonte: Wikimedia.com

O sistema que utilizamos hoje é um sistema decimal posicional, no número 297 observamos que o 2 não tem valor igual a dois, pois a sua posição é a da centena, assim também é com o número 9 que está na posição das dezenas, já o 7 possui o valor do próprio algarismo porque ocupa a posição das unidades. Uma forma de entender como o sistema decimal é utilizado é através das potencias de base 10. O número 297 pode ser escrito da seguinte maneira: 2 x 10² +  9 x 10^{1 +} 7 x 10⁰  que é igual a 297 no sistema decimal. Nosso sistema, assim como o sistema dos babilônios, é um sistema aditivo. Como ficaria o número 297 no sistema sexagesimal? Podemos fazer uma “tradução”: 2 x 60² +  9 x 60^{1 +} 7 x 60⁰  que é igual a 7747 no sistema decimal.

Obviamente com a falta de símbolos o sistema de numeração dos babilônios apresentaram problemas. Na tabela abaixo podemos observar que com um mesmo símbolo podemos escrever vários números. Como distinguir?

Tabela 01 - Conversão de Símbolos. 

Em um momento os babilônios utilizavam um símbolo maior para representar o 60 e um símbolo menor para representar o 1. Após a padronização dos símbolos eles começaram a deixar um espaço vazio entre os números, semelhantemente ao zero que utilizamos no sistema indo-arábico para diferenciar 11 de 101. Mais tarde os escribas desenvolveram o símbolo   como um separador, assim como fazemos com o zero, mas ele não tinha a função de representar a quantidade zero.

Os babilônios desenvolveram a matemática em um nível muito elevado. Tabletes de cerâmica revelam que eles resolviam as quatro operações básicas, além da potenciação e raízes quadradas. Resolviam também problemas que envolviam equações. Seus métodos não eram como os nossos. Eles utilizavam conceitos de comprimento, largura e áreas. Havia também problemas de investigação sobre formas, áreas e volumes.

Podemos, portanto, concluir que os babilônios desenvolveram a matemática em um nível muito elevado, pois os tabletes de cerâmica revelam que eles resolviam as quatro operações básicas, além da potenciação e raízes quadradas. Observamos também a resolução de problemas que envolviam equações e a utilização de conceitos de comprimento, largura e áreas, com até mesmos problemas de investigação de formas, áreas e volumes. Seus métodos não eram como os nosso, mas possuem um valor inestimável para a história da matemática moderna.

REFERÊNCIAS

FLOOD, raymond. A História dos Grandes Matemáticos. 1.ª Edição, São Paulo, EditoraM. Books do Brasil, 2013.

ROQUE, Tatiana. História da Matemática: uma visão crítica, desfazendo mitos e lendas. 1.ª Edição, Rio de Janeiro, Editora Zahar, 2012.