 |
| Figura 01- Arquimedes. Fonte www.educ.fc.ul.pt3 |
O homem sempre buscou na natureza recursos que pudessem facilitar sua vida e, desde a idade da pedra, vem desenvolvendo artefatos que o auxiliam de alguma maneira em seu dia a dia. As alavancas nada mais são do que mais uma façanha do homem para realizar tarefas cada vez mais difíceis.
O mérito da invenção e principalmente da explicação do funcionamento das alavancas é sempre relacionado a Arquimedes, ele teria sido o inventor e primeiro a utilizá-las com grande sucesso.
Arquimedes é considerado um dos maiores matemáticos da antiguidade, viveu de 287 a 212 a.C. quase toda a vida em Siracusa, na costa da Sicília, atual Itália. Um de seus trabalhos mais famosos é relacionado ao empuxo, mas a utilização e explicação do funcionamento das alavancas foi também de grande importância.
A ideia da alavanca é utilizar um braço mecânico (que pode ser uma haste comprida) suspensa em um ponto de apoio, este funcionará como um eixo para que ela possa girar, formando então uma gangorra. Em uma das extremidades deve-se suspender uma carga ou peso, algo que se quer levantar, e na outra exercer uma força. Assim dependendo da distância entre o peso e o eixo, e entre a força aplicada e o eixo, poderemos com uma força pequena levantar grandes pesos.
Arquimedes tem uma frase bastante famosa relacionada as suas invenções mecânicas e sua capacidade de mover grandes pesos realizando pouca força: “Dê-me um ponto de apoio e moverei a Terra!”
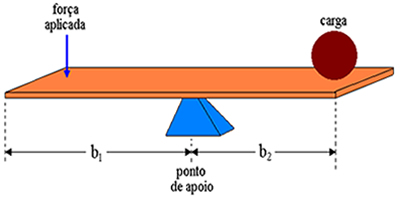 |
Figura 2 – alavanca. Fonte: www.alunosonline.com.br
|
Para entender como uma alavanca funciona precisamos entender o conceito de torque, um conceito físico bastante importante quando queremos descrever sistemas dinâmicos.
O torque é a tendência à rotação, ou seja, a “vontade que algo tem de girar”. Por exemplo, ao empurrar uma porta para fechá-la, estamos causando um torque na porta, e ela então irá rotacionar em volta de seu eixo até fechar.
O torque depende da força aplicada e da distancia do eixo de rotação. Quanto maior a força aplicada na porta, por exemplo, e maior a distância entre o eixo de rotação e o ponto de aplicação da força, maior será o Torque, ou seja, mais facilmente ela irá fechar!
Tente fechar a porta empurrando bem perto do eixo de rotação...Isso fará o torque diminuir conseqüentemente será bem mais difícil fechá-la.
 |
| Figura 03 – Torque na Porta. Fonte: fisicaeplaneta.blogspot.com.br |
Podemos escrever o torque como:
T = F.d
Onde
F= força
d = distância ( no desenho esta representado por b)
Uma alavanca tem dois lados:
LADO1 => onde será aplicada a força
LADO 2 => onde será sustentado o peso que se quer levantar.
Temos dois torques para analisar, T1 e T2, lembrando que por definição troque é a tendência a rotacionar. Sabemos que a haste é um corpo rígido, portanto, não há como uma parte girar mais do que outra, logo o torque nos dois lados deve ser igual, mas as forças e a posição onde foram aplicadas podem ser diferentes.
Imagine uma haste de um metro. No lado 2 iremos colocar uma massa de 10kg a uma distância de 50cm do eixo de rotação, ou seja, exatamente na extremidade da haste. Também na extremidade, mas agora no lado 1, quanta força devemos aplicar para levantar o peso???
T = Torque
F = Força
d = Distância do objeto ao eixo.
Vamos calcular!
Usando o que sabemos sobre torque:
T1
= T2
F1*d1 = F2*d2
como
d1= d2 então F1 = F2
Ou seja, se as distâncias forem iguais então as forças também serão! Mas e se colocarmos uma massa de 10 kg a 25cm do eixo de rotação?
T1
= T2
F1*d1
= F2*d2
***lembrando que usaremos as medidas em metros e força = massa*aceleração!
F2=10kg*10m/s2
, F2 = 100N
Teremos
F1*0,5m = 100N * 0,25m
F1
= (100N * 0,25m ) / 0,5
F1
= 50N
Ou seja, com uma força de apenas 50N, conseguimos levantar um peso de 100N!
Mostramos então que a alavanca pode ser muito eficiente. Mas, será que Arquimedes estava certo em pensar que uma pessoa poderia mover algo tão pesado quanto a Terra?
Se for possível, qual o tamanho da alavanca?
A massa da terra corresponde a aproximadamente 6*10^24 kg. Imaginemos então levantar algo com esse peso num local onde a gravidade é próxima a gravidade da terra (10m/s^2), ou seja, uma força peso de 60*10^24N. Uma pessoa adulta tem em media 80Kg, imaginando que irá apenas usar a força de seu peso então temos uma força de 800N.
 |
Figura 4. Levantando o Mundo. Fonte: brincandocomafisicaequimica.blogspot.com
|
Temos:
T1=T2
F2
= Peso da terra 60*10^24N.
F1
= Peso da pessoa 800 N
F1*d1
= F2*d2
800N
*d1 = 60*10^24N * d2
d1
= (60*10^24N * d2 )/ 800N
d1
= 0,75 * 10^23 *d2
Para que possamos levantar a terra, a distancia d2 deve ser 0,75*10^23 vezes maior que a distancia d1, ou seja, 7500000000000000000000000 vezes maior. Se a distancia d1 = 1 metro então a distancia d2 será 7500000000000000000000000.
Levantar a terra é com certeza uma situação hipotética, mas o uso das alavancas não, hoje elas são utilizadas em diversas situações reais para levantar objetos pesados e facilitar os mais diversos trabalhos.
REFERÊNCIAS
Magnaghi, Ceno Pietr. Análise e Tradução Comentada da Obra de Arquimedes Intitulada "MÉTODO SOBRE OS TEOREMAS MECÂNICOS". Disponível em: http://www.ifi.unicamp.br/~assis/tese-Ceno.pdf

2 Comentários
a última questão sobre Arquimedes e o erguimento da terra está com erro de digitação.Certo seria: ''Para que possamos levantar a terra, a distancia d1 deve ser 0,75*10^23 vezes maior que a distancia d2, ou seja, 7500000000000000000000000 vezes maior. Se a distancia d2 = 1 metro então a distancia d1 será 7500000000000000000000000.''
ResponderExcluirtop loko
ResponderExcluir